Skip to contents

Forecast for iAR, CiAR, and BiAR Classes

forecast.Rd

Generates forecasts for the specified time series model. This method is implemented for: 1. Irregular Autoregressive models (`iAR`) 2. Complex Irregular Autoregressive models (`CiAR`) 3. Bivariate Autoregressive models (`BiAR`)

Usage

forecast(x, ...)

Arguments

x

An object of class iAR, CiAR, or BiAR, containing the model specification and parameters:

  • For iAR:

    • family: The distribution family of the iAR model (one of "norm", "t", or "gamma").

    • series: A numeric vector representing the time series to forecast.

    • coef: The coefficient(s) of the iAR model.

    • zero_mean: Logical, whether the model assumes a zero-mean series.

    • standardized: Logical, whether the model uses standardized data (only for "norm" family).

    • mean: The mean parameter (only for "gamma" family).

    • tAhead: Integer, the number of steps ahead to forecast.

  • For CiAR:

    • coef: The real and imaginary parts of the CiAR model's coefficients.

    • series: A numeric vector representing the time series to forecast.

    • times: A numeric vector specifying the time points of the series.

    • zero_mean: Logical, whether the model assumes a zero-mean series.

    • standardized: Logical, whether the model output should be standardized.

    • tAhead: Integer, the number of steps ahead to forecast.

  • For BiAR:

    • coef: The coefficients of the BiAR model (real and imaginary parts).

    • series: A numeric matrix with two columns representing the bivariate time series to forecast.

    • times: A numeric vector specifying the time points of the series.

    • tAhead: Integer, the number of steps ahead to forecast.

...

Additional arguments (unused).

Value

An updated object of class iAR, CiAR, or BiAR, where the forecast property contains the forecasted values.

Details

This method generates forecasts for the specified time series model. Depending on the class of the input object:

  • For iAR, the function supports three distribution families:

  • "norm" for normal distribution.

  • "t" for t-distribution.

  • "gamma" for gamma distribution.

  • For CiAR, the function uses complex autoregressive processes.

  • For BiAR, the function generates forecasts for a bivariate autoregressive process.

All required parameters (e.g., coefficients, time points) must be set before calling this method.

References

Eyheramendy S, Elorrieta F, Palma W (2018). “An irregular discrete time series model to identify residuals with autocorrelation in astronomical light curves.” Monthly Notices of the Royal Astronomical Society, 481(4), 4311-4322. ISSN 0035-8711, doi:10.1093/mnras/sty2487 , https://academic.oup.com/mnras/article-pdf/481/4/4311/25906473/sty2487.pdf. ,Elorrieta, F, Eyheramendy, S, Palma, W (2019). “Discrete-time autoregressive model for unequally spaced time-series observations.” A&A, 627, A120. doi:10.1051/0004-6361/201935560 . ,Elorrieta F, Eyheramendy S, Palma W, Ojeda C (2021). “A novel bivariate autoregressive model for predicting and forecasting irregularly observed time series.” Monthly Notices of the Royal Astronomical Society, 505(1), 1105-1116. ISSN 0035-8711, doi:10.1093/mnras/stab1216 , https://academic.oup.com/mnras/article-pdf/505/1/1105/38391762/stab1216.pdf.

Examples

# Example 1: Forecasting with a normal iAR model
library(iAR)
n=100
set.seed(6714)
o=iAR::utilities()
o<-gentime(o, n=n)
times=o@times
model_norm <- iAR(family = "norm", times = times, coef = 0.9)  
model_norm <- sim(model_norm)
model_norm <- kalman(model_norm) 
model_norm@tAhead=1.3
model_norm <- forecast(model_norm)
plot(times, model_norm@series, type = "l", main = "Original Series with Forecast")
points(max(times)+ model_norm@tAhead, model_norm@forecast, col = "blue", pch = 16)

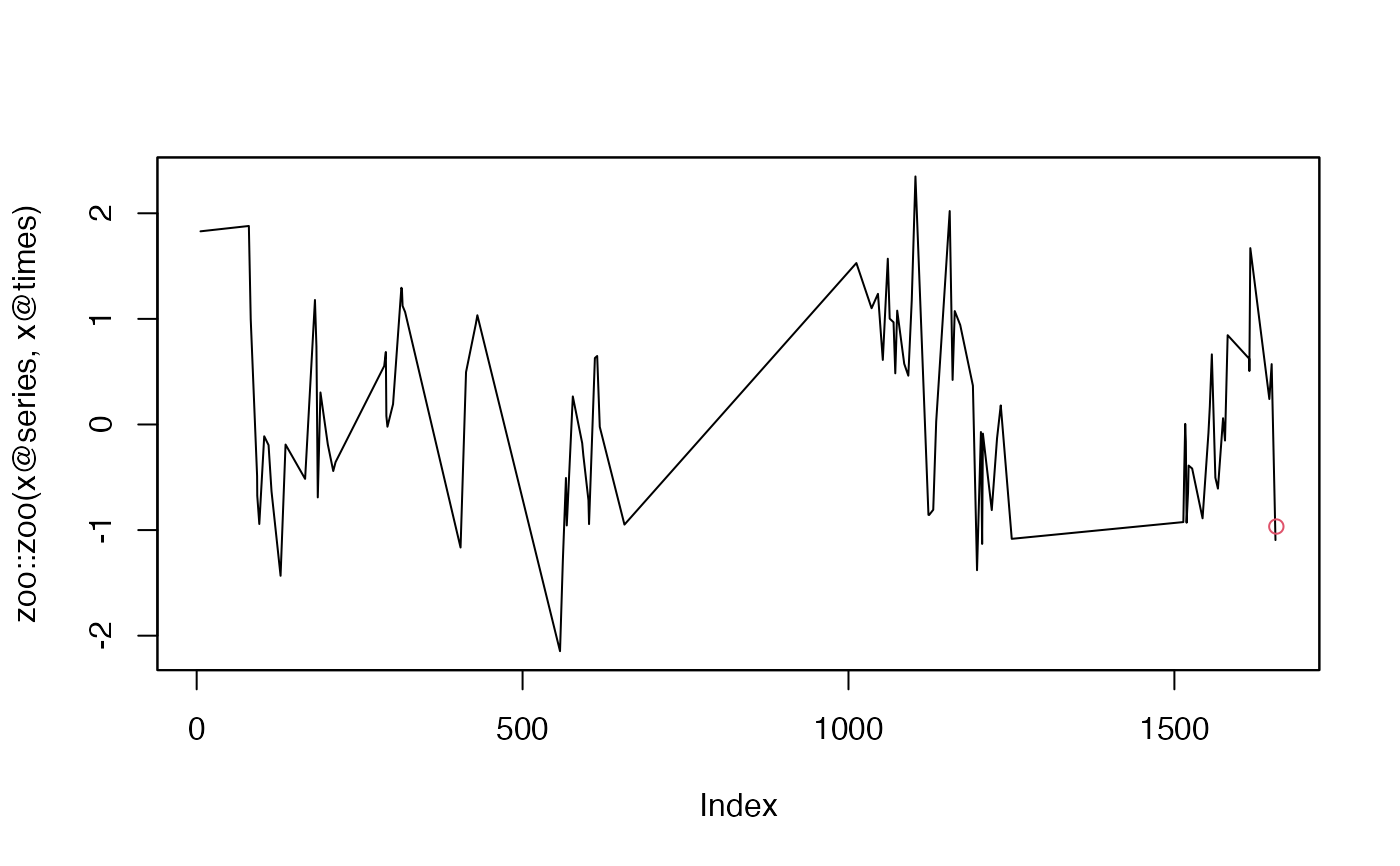
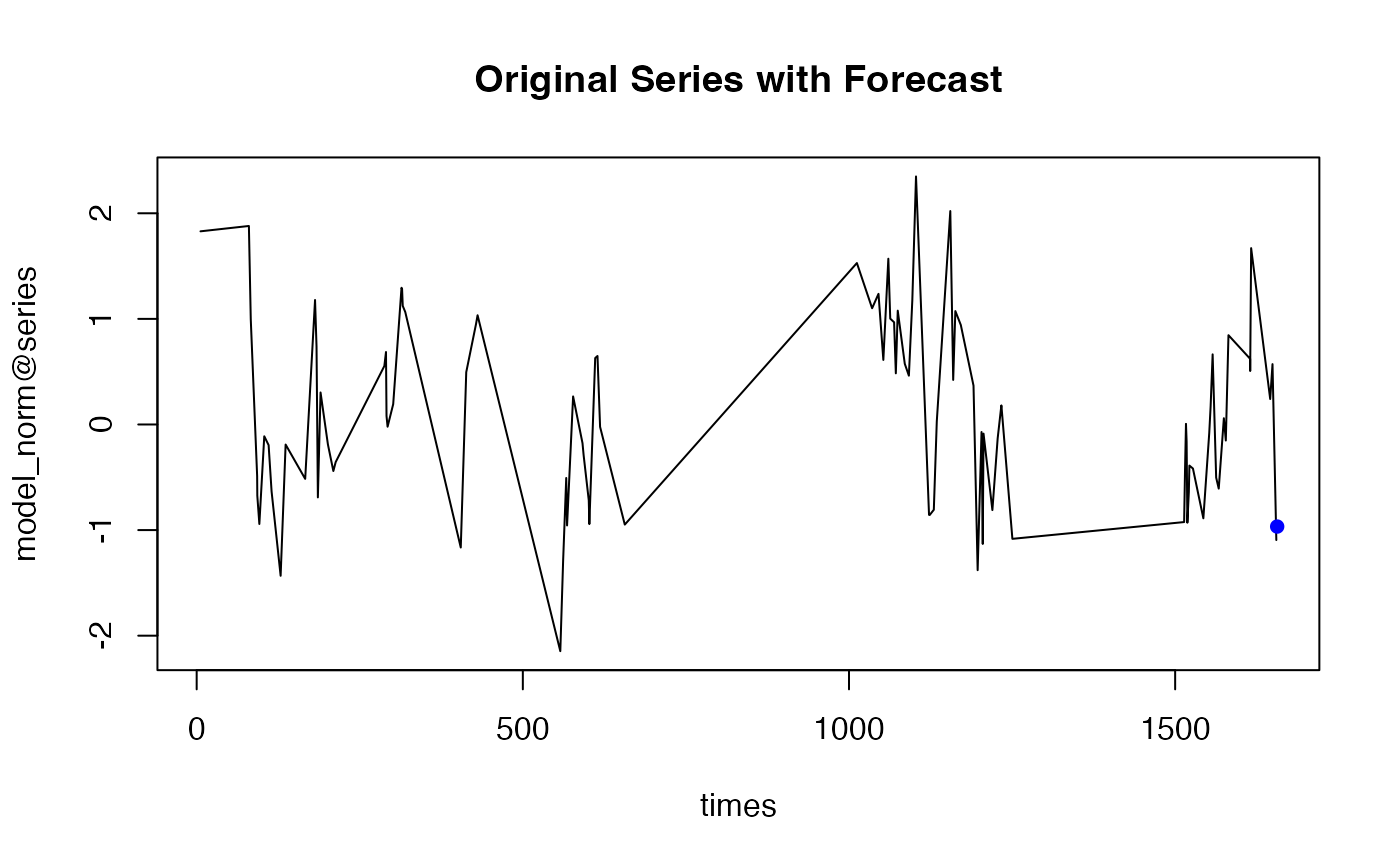plot_forecast(model_norm)


# Example 2: Forecasting with a CiAR model
set.seed(6714)
model_CiAR <- CiAR(times = times,coef = c(0.9, 0))
model_CiAR <- sim(model_CiAR)
y=model_CiAR@series
y1=y/sd(y)
model_CiAR@series=y1
model_CiAR@series_esd=rep(0,n)
model_CiAR <- kalman(model_CiAR)
print(model_CiAR@coef)
#> [1] 0.9199923 0.1072453
model_CiAR@tAhead=1.3
model_CiAR <-forecast(model_CiAR)
model_CiAR@forecast
#> [1] 0.2925816

# Example 3: Forecasting with a BiAR model
n=80
set.seed(6714)
o=iAR::utilities()
o<-gentime(o, n=n)
times=o@times
model_BiAR <- BiAR(times = times,coef = c(0.9, 0.3), rho = 0.9)
model_BiAR <- sim(model_BiAR)
y=model_BiAR@series
y1=y/apply(y,2,sd)
model_BiAR@series=y1
model_BiAR@series_esd=matrix(0,n,2)
model_BiAR <- kalman(model_BiAR)
print(model_BiAR@coef)
#> [1] 0.9061971 0.3054558
model_BiAR@tAhead=1.3
model_BiAR <-forecast(model_BiAR)
model_BiAR@forecast
#>            [,1]     [,2]
#> [1,] -0.2210477 2.414699